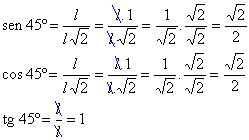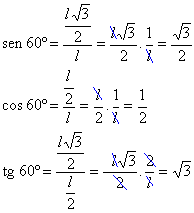EQUAÇÕES LITERAIS Chama-se equação literal a uma equação onde aparecem uma ou mais letras para além da incógnita. Para resolver uma equação literal, decide-se qual é a incógnita e consideram-se as outras letras como se fossem números conhecidos (parâmetros). Ex. Considere um rectângulo de dimensões x e y e escreva uma formula para: determinar o perímetro p, conhecidos x e y; determinar x, conhecidos p e y.

Resolução: A fórmula p = 2x + 2y permite determinar o perímetro p, conhecidos x e y. Para determinar x, conhecidos p e y, partimos da equação p = 2x + 2y e resolvemo-la em ordem a x, isto é, consideramos x como incógnita. p= 2x + 2y Û - 2x = - p + 2y Û 2x = p – 2y Û

EQUAÇÕES DE 2º GRAU

DEFINIÇÕES:

As equações do 2º grau ou equações quadráticas são da forma
ax² + bx + c = 0, em que a, b e c são números reais e a ¹ 0.

a é o coeficiente de x²

b é o coeficiente de x e c é o termo independente.

Uma equação diz-se completa se b e c são diferentes de zero;

caso contrário, temos uma equação incompletas.

Quando uma equação do 2º grau tem a forma ax² + bx + c = 0,

diz-se que está na forma canónica.

EQUAÇÕES COMPLETAS

Como foi referido temos uma equação completa se b e c são diferentes de zero. Este tipo de equação resolve-se através da fórmula resolvente, que permite obter, mais rapidamente as soluções de qualquer equação do 2º grau. Vamos deduzir a formula resolvente, a partir da equação ax2 + bx + c = 0, a ¹ 0

A resolução desta equação conduziu-nos à FÓRMULA RESOLVENTE DAS EQUAÇÕES DE 2º GRAU:

É chamado o binómio discriminante. Sendo muito útil para determinarmos quantas soluções têm as equações de 2º grau. A equação não tem soluções reais. A equação tem uma só solução real. A equação tem duas soluções reais.

EQUAÇÕES INCOMPLETAS

Uma equação do 2º grau será incompleta se se verificar um dos três casos
como possíveis.

EQUAÇÕES INCOMPLETAS ax² = 0 com b = 0 e c = 0
ax² + c = 0 com b = 0
ax² + bx = 0 com c = 0

Caso em que b = 0 e c = 0

Consideremos a equação 2x² = 0 Û
Û x² = 0 Û
Û x = 0

Caso em que b = 0

Por exemplo a equação 3x² - 12 = 0 Û
Û 3x² =12 Û
Û x² = 12/3 Û
Û x² = 4 Û
Û x = 2 ٧ x = -2

Caso em que c = 0

Consideremos a equação 3x² + 7x = 0.
Para resolvermos esta equação temos de aplicar a lei do anulamento do produto.

LEI DO ANULAMENTO DO PRODUTO Um produto é nulo se e só se pelo menos um dos seus factores é nulo. Simbolicamente: ab = 0 Û a = 0 ٧ b = 0 abc = 0 Û a = 0 ٧ b = 0 ٧ c = 0 ...

Pomos x em evidência e aplicamos a lei do anulamento do produto:
x (3x + 7) = 0 Û x = 0 ٧ 3x + 7 = 0 Û x= 0 ٧ x = -7/3

EQUAÇÕES DE 3º GRAU

As equações de 3º grau ou equações cúbicas são da forma: ax3 + bx2 + cx + d = 0, a ¹ 0 a é o coeficiente de x3 b é o coeficiente de x2 c é o coeficiente de x d é o termo independente

Vamos ver os vários casos possíveis de resolução:

CASOS POSSÍVEIS	MODOS DE RESOLUÇÃO
d = 0 ax3 + bx2 + cx = 0	põe-se x em evidência; lei do anulamento do produto; formula resolvente.
c = 0 ax3 + bx2 + d = 0	regra de Ruffini; formula resolvente.
b = 0 ax3 + cx + d = 0	regra de Ruffini; formula resolvente.
b = 0 c = 0 ax3 + d = 0	resolve-se da forma usual.
b = 0 d = 0 ax3 + cx = 0	põe-se x em evidência; lei do anulamento do produto; se c > 0 então a equação é impossível e se c < 0 então a equação tem duas soluções.
c = 0 d = 0 ax3 + bx2 = 0	põe-se x2 em evidência; lei do anulamento do produto; resolve-se da forma usual.
b = 0 c = 0 d = 0 ax3 = 0	resolve-se da forma usual.
b, c, d ¹ 0 ax3 + bx2 + cx + d = 0	regra de Ruffini; lei do anulamento do produto; fórmula resolvente.

Racionalização de denominadores

Elimine raiz do "pé" da fração

Carlos Alberto Campagner*
Especial para a Página 3 Pedagogia & Comunicação

Em alguns cálculos, você pode se deparar com raízes no denominador da fração. Para que você possa prosseguir com os cálculos, é conveniente que você elimine essas raízes do denominador - processo chamado de racionalização de denominadores. Isto é, transforma-se um denominador irracional em racional.

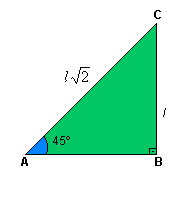
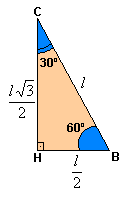
o denominador é um número irracional e deve ser eliminado.

Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.

Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por ficará:

. Note que é igual a 1, logo a multiplicação de um número por 1 não o altera.

Prosseguindo:




Como se pode notar o denominador agora é um número racional (3).

Raízes não-quadradas

Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz quadrada é, na verdade, uma raiz de índice 2!), é necessário utilizar um artifício.




Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original menos um. Por exemplo:

Soma de raízes no denominador

Veja:




Deve-se multiplicar por .

Isso porque a multiplicação de por é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a² + b²) - isto é, os radicais somem!

*Carlos Alberto Campagner é engenheiro mecânico, com mestrado em mecânica, professor de pós-graduação e consultor de informática

As razões trigonométricas de 30º, 45º e 60º

Considere as figuras:

quadrado de lado l e diagonal

Triângulo eqüilátero de lado I e altura

Seno, cosseno e tangente de 30º

Aplicando as definições de seno, cosseno e tangente para os ângulos de 30º, temos:

Seno, cosseno e tangente de 45º

Aplicando as definições de seno, cosseno e tangente´para um ângulo de 45º, temos:

Seno, cosseno e tangente de 60º

Aplicando as definições de seno, cosseno e tangente para um ângulo de 60º, temos:

Resumindo

x	sen x	cos x	tg x
30º
45º
60º